1. Tujuan [Kembali]
- Untuk memahami karakteristik rangkaian active filters
- Untuk mengetahui bagaimana cara merangkai rangkaian active filters
- Dapat mensimulsikan rangkaian active filters
2. Alat dan Bahan [Kembali]
- Alat
a. Instrumen
Osiloskop
Osiloskop digunakan untuk mengamati bentuk gelombang input dan output pada rangkaian.
Osiloskop adalah komponen elektronika yang mempunyai kemampuan menyimpan electron-elektron selama waktu yang tidak tertentu. Osiloskop
dilengkapi dengan tabung sinar katode. Peranti pemancar elektron
memproyeksikan sorotan elektron ke layar tabung sinar katode.
Pinout:
b. Generator
VSINE, berfungsi sebagai sumber arus listrik AC.
- Bahan
1. Resistor, berfungsi sebagai pembagi, pembatas, dan pengatur arus dalam suatu rangkaian.
Resistor merupakan salah satu komponen elektronika pasif yang berfungsi untuk membatasi arus yang mengalir pada suatu rangkaian dan berfungsi sebagai terminal antara dua komponen elektronika. Tegangan pada suatu resistor sebanding dengan arus yang melewatinya
Resistor berfungsi untuk menghambat arus dalam rangkaian listrik. Cara menghitung nilai resistansi resistor dengan gelang warna:
1. Masukan angka langsung dari kode warna gelang pertama.
2. Masukan angka langsung dari kode warna gelang kedua.
3. Masukan angka langsung dari kode warna gelang ketiga.
4. Masukkan jumlah nol dari kode warna gelang ke-4 atau pangkatkan angka tersebut dengan 10 (10^n), ini merupakan nilai toleransi dari resistor.
.png)
2. Kapasitor, berfungsi sebagai tempat penyimpan arus dan tegangan.
Cara menentukan:Nilai kapasitor (104J) : 10 * 10^4 pF = 10^5 pF = 100nF; toleransi 5% = ± 95nF sampai 105nF
Kapasitor adalah komponen elektronika pasif yang dapat menyimpan muatan listrik dalam waktu sementara.
Cara menghitung nilai kapasitor :
1. Masukan 2 angka pertama langsung untuk nilai kapasitor.
2. Angka ke-3 berfungsi sebagai perpangkatan (10^n) nilai kapasitor.
3. Satuan kapasitor dalam piko farad.
4. Huruf terakhir menyatakan nilai toleransi dari kapasitor.Daftar nilai toleransi kapasitor :
B = 0.10pF
C = 0.25pF
D = 0.5pF
E = 0.5%
F = 1%
G = 2%
H = 3%
J = 5%
K = 10%
M = 20%Z = + 80% dan -20%
Pinout:
Spesifikasi:
3. Op-amp, berfungsi sebagai pengindra dan penguat sinyal masukan baik DC maupun AC juga sebagai penguat diferensiasi impedansi masukan tinggi, penguat keluaran impedansi rendah.
Konfigurasi PIN LM741
3. Dasar Teori [Kembali]
Sirkuit filter dapat dibangun menggunakan komponen pasif : resistor dan kapasitor. Dan juga menggunakan amplifier untuk memberikan penguatan tegangan dan isolasi sinyal atau buffering.
Gambar 15.30 Respon filter ideal (a) low pass (b) High pass (c) Band pass
1) Filter active low pass
Menggunakan resistor tunggal dan kapasitor seperti pada gambar 15.31a memiliki kemiringan praktis 20 dB per dekade. Gambar 15.31b adalah respon ideal dari gambar 15.31a.
Pada frekuensi cuttof dari :
Gambar 15.31 Filter aktif low-pass orde pertama
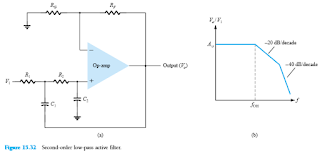
Gambar 15.32 Filter aktif low-pass orde kedua
2) Filter active high pass
Frekuensi cutoff amplifier:
Gambar 15.33 High Pass Filter
3) Filter Bandpass
Sebuah band-pass filter merupakan perangkat yang melewati frekuensi dalam kisaran tertentu dan menolak (attenuates) frekuensi di luar kisaran tersebut. Contoh dari analog elektronik band pass filter adalah sirkuit RLC (a resistor-induktor-kapasitor sirkuit). Filter ini juga dapat dibuat dengan menggabungkan filter-pass rendah dengan filter - pass tinggi.
Gambar 15.34 Band Pass Filter
Example
1.Hitung frekuensi cutoff dari filter-rendah orde pertama untuk R1 1,2 k dan
C1 0,02 microF.
R1 5 R2 5 2.1 kV, C1 5 C2 5 0.05 mF, dan Ro1 5 10 kV, Rof 5 50 kV.
SOLUSI
Menerapkan hukum tegangan Kirchhoff ke sirkuit input akan
Menerapkan hukum tegangan Kirchhoff ke sirkuit output akan
Semua
contoh sejauh ini telah menggunakan konfigurasi common-emitter atau
commoncollector. Dalam contoh berikutnya kami menyelidiki konfigurasi
common-base. Dalam situasi ini sirkuit input akan digunakan untuk
menentukan IE daripada Ib. Arus kolektor kemudian tersedia untuk
melakukan analisis sirkuit output.
SOLUSI
Menerapkan hukum tegangan Kirchhoff ke sirkuit input akan
Contoh 4.18 menggunakan pasokan terpisah dan akan memerlukan aplikasi untuk menentukan yang diinginkan tidak diketahui.
SOLUSI
Ketahanan
dan tegangan Thévenin ditentukan untuk jaringan di sebelah kiri
terminal dasar seperti yang ditunjukkan pada Buah Ara. 4.44 dan 4.45.
Jaringan
kemudian dapat digambar ulang seperti yang ditunjukkan dalam Gbr. 4.46,
di mana aplikasi Hukum tegangan Kirchhoff akan menghasilkan
Pilihan Soal Ganda
1. Hitung frekuensi cutoff dari filter low-pass orde pertama untuk R1= 1.2 kOhm dan C1 = 0.02 mF.
a) 6.63 kHz
b) 3.23 kHz
c) 7.98 kHz
d) 4.56 kHz
Jawaban : a) 6.63 kHz
2. Hitung foL dari rangkaian filter bandpass pada gambar 15.34 dengan R1=R2= 10 kOhm , C1= 0.1 mF dan C2= 0.002 mF.
a) 267.76 Hz
b) 159.15 Hz
c) 234.09 Hz
d) 436.89 Hz
Jawaban : b) 159.15 Hz
3. Hitung foH dari rangkaian filter bandpass pada gambar 15.34 dengan R1=R2= 10 kOhm , C1= 0.1 mF dan C2= 0.002 mF.
a) 7.96 kHz
b) 8.78 kHz
c) 6.89 kHz
d) 5.43 kHz
Jawaban : a) 7.96 kHz
4. Percobaan [Kembali]
a. Prosedur Percobaan
- Mempersiapkan Alat besrta Bahan seperti yang telah tertera pada Sub Bab Alat dan Bahan di atas
- Merangkai Rangkaian sesuai dengan jenisnya masing-masing, terdapat 8 jenis rangkaian yang akan diujikan.
- Pada masing-masing Rangkaian disambungkan input tegangan AC agar dapat melihat bagaimana perbedaan respons gelombang input dan outputnya.
- Amatilah nilai input dan output dengan menyesuaikannya dengan rumus yang ada, dan juga amatilah respon grafik sinyal input dan outputnya.
b. Rangkaian Simulasi dan Prinsip Kerja
.png)
Gambar Rangkaian 15.31
15.31
Suatu
filter lolos bawah orde satu dapat dibuat dari satu tahanan dan satu
kapasitor. Arus input masuk ke R1 sebesar 1,6k yang paralel dengan
kapasitor sebesar o,1 mikroFarad. untuk mencari frekuensi, f= 1/2phiRC.
sebelumnya kita mencari WC = 1/RC dan didapatkan hasil sekitar 6250 pada
frekuensi, sehingga db akan dapat dilihat pada tabel grafik frekuensi.
Filter orde satu ini mempunyai pita transisi dengan
kemiringan -20 dB/dekade atau –6 dB/oktav. Penguatan tegangan untuk
frekuensi lebih rendah dari frekuensi cut off adalah: Av = - R2 / R1
sementara besarnya frekuensi cut off didapat dari: fC = 1 / (2.R2C1). Hasil
dari rumus ini mendapatkan frekuensi dan dapat dilihat dB pada tabel
grafik frekuensi respon, gelombang low pass filter dapat dilihat pada
osiloskop.
.png)
Gambar Rangkaian 15.32
15.32 Suatu
filter lolos bawah orde dua dapat dibuat dari dua tahanan dan dua
kapasitor. Arus input masuk ke R1 sebesar 1,6k yang paralel dengan C1 sebesar
o,1 mikroFarad. kemudian mengalir masuk ke R2 sebesar 10k yang paralel dengan C2
sebesar o,1 mikroFarad. untuk mencari frekuensi, f= 1/2phiRC. sebelumnya
kita mencari WC = 1/RC dan didapatkan hasil sekitar 6250 pada
frekuensi, sehingga db akan dapat dilihat pada tabel grafik frekuensi.
Filter orde satu ini mempunyai pita transisi dengan
kemiringan -20 dB/dekade atau –6 dB/oktav. Penguatan tegangan untuk
frekuensi lebih rendah dari frekuensi cut off adalah: Av = - R2 / R1
sementara besarnya frekuensi cut off didapat dari: fC = 1 / (2.R2C1). Hasil
dari rumus ini mendapatkan frekuensi dan dapat dilihat dB pada tabel
grafik frekuensi respon, gelombang low pass filter dapat dilihat pada
osiloskop.
.png)
Gambar Rangkaian 15.33 (a)
15.33 (A) Suatu
filter lolos atas orde satu dapat dibuat dari satu tahanan dan satu
kapasitor. Arus akan mengalir menuju C1 sebesar 0,1 mikroFarad yang
paralel dengan R1 sebesar 22k dan menuju ke kaki non inverting op amp.
Filter orde satu ini mempunyai pita transisi dengan
kemiringan 20 dB/dekade atau 6 dB/oktav. Penguatan tegangan untuk
frekuensi lebih tinggi dari frekuensi cut off adalah: Av = - R2 / R1
sementara besarnya frekuensi cut off didapat dari: fC = 1 / (2.R1C1).
Hasil dari rumus ini mendapatkan frekuensi dan dapat dilihat dB pada
tabel grafik frekuensi respon, gelombang high pass filter dapat dilihat
pada osiloskop.
.png)
Gambar Rangkaian 15.33 (b)
15.33 (B) Suatu
filter lolos atas orde satu dapat dibuat dari satu tahanan dan satu
kapasitor. Arus akan mengalir menuju C1 sebesar 0,1 mikroFarad yang
paralel dengan R1 sebesar 22k dan mengalir menuju C2 sebesar 0,1
mikroFarad yang paralel dengan R1 sebesar 22k dan menuju ke kaki non
inverting op amp. Filter orde satu ini mempunyai pita transisi dengan
kemiringan 20 dB/dekade atau 6 dB/oktav. Penguatan tegangan untuk
frekuensi lebih tinggi dari frekuensi cut off adalah: Av = - R2 / R1
sementara besarnya frekuensi cut off didapat dari: fC = 1 / (2.R1C1).
Hasil dari rumus ini mendapatkan frekuensi dan dapat dilihat dB pada
tabel grafik frekuensi respon, gelombang high pass filter dapat dilihat
pada osiloskop.
.png)
Gambar Rangkaian 15.34
15.34 Rangkaian Band Pass Filter memiliki penggabungan dari low pass filter dan high pass filter dengan arus input mengalir menuju R3 sebesar 330 yang paralel dengan C1 sebesar 0,1 nF dan menuju kaki non inverting op amp. Kemudian arus mengalir menuju C2 sebesar 0,1 nF yang paralel dengan R4 sebesar 10k dan menuju kaki non inverting op amp. Penguatan tegangan untuk pita lolos adalah: Av = (-R2 / R1) (-R4 / R3) Besarnya frekuensi cut off atas didapat dari: fCH = 1 / (2.R1C1) Besarnya frekuensi cut off bawah didapat dari: fCL = 1 / (2.R4C2). Hasil dari rumus ini mendapatkan frekuensi dan dapat dilihat dB pada tabel grafik frekuensi respon, gelombang high pass filter dapat dilihat pada osiloskop.
c. Video
15.31 Rangkaian Low Pass Filter First Order
15.32 Rangkaian Low Pass Filter Second Order
15.33 (a) Rangkaian High Pass Filter First Order
15.33 (b) Rangkaian High Pass Filter Second Order
15.34 Rangkaian Band Pass Filter
Download materi silahkan klik Disini
Download HTML silahkan klik Disini
Download Datasheet Resistor silahkan klik Disini
Download Datasheet OP-AMP silahkan klik Disini
Download Datasheet Kapasistor silahkan klik Disini
Download bentuk rangkaian 15.31 silahkan klik Disini
Download bentuk rangkaian 15.32 silahkan klik Disini
Download bentuk rangkaian 15.33 (a) silahkan klik Disini
Download bentuk rangkaian 15.33 (b) silahkan klik Disini
Download bentuk rangkaian 15.34 silahkan klik Disini
Download video simulasi rangkaian 15.31 silahkan klik Disini
Download video simulasi rangkaian 15.32 silahkan klik Disini
Download video simulasi rangkaian 15.33 (a) silahkan klik Disini
Download video simulasi rangkaian 15.33 (b) silahkan klik Disini
Download video simulasi rangkaian 15.34 silahkan klik Disini
Tidak ada komentar:
Posting Komentar